Pentominous U-Bahn

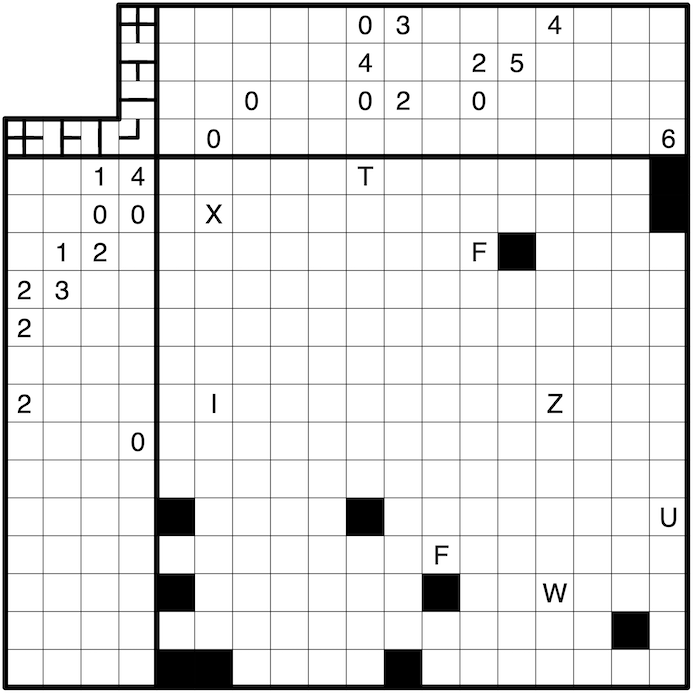
Rules:

Tessellate the entire grid besides the black cells into pentominos (orthogonally connected regions of exactly five cells) such that no two pentominos of the same shape share an edge. Rotations and reflections of a shape are counted as the same shape. A cell with a letter indicates the shape of the pentomino that contains that cell.

Draw a totally connected loop network through the centers of some cells, which may branch or turn, but may not have any dead ends. A clue outside the grid indicates how many times the corresponding line shape (i.e. a cross, branch, straight line, or turn) appears in the corresponding row or column, irrespective of the line shape’s rotation. The loop network may enter the black cells freely.

Every pentomino must satisfy one of the two following conditions:

One Shape:

All non-empty cells within the pentomino must be the same line shape. Two pentominos satisfying this condition may never be orthogonally adjacent.

All Shapes:

The pentomino must contain one turn, one straight, one branch, one cross, and one empty cell.